Introduction

Detokenization is the reverse operation of tokenization, which is where an input character sequence is split into pieces called tokens. One possible approach to implementing a detokenizer is to build a basic statistical machine translation (SMT) system whose purpose is to translate from tokenized to raw text. For such a system to work we need first to train the language and phrase translation statistical models. Once the model parameters are estimated, we can use them to generate translations, i.e. detokenized texts, in the so-called decoding process.

In part I of this article, we saw how language and phrase models for detokenization can be estimated. In this second part we explain how these models are applied during decoding.

Decoding for Statistical Machine Translation

During the decoding stage, SMT systems use the knowledge contained in their statistical models to infer the translations for the input sentences.

A given sentence can be translated in many ways depending on the translation options for each segment contained in the phrase model. Below we show how the Spanish sentence x: material excelente para diversos usos is translated into the English sentence y: excellent material for different purposes by choosing a specific set of translation options stored in a hypothetical phrase model.

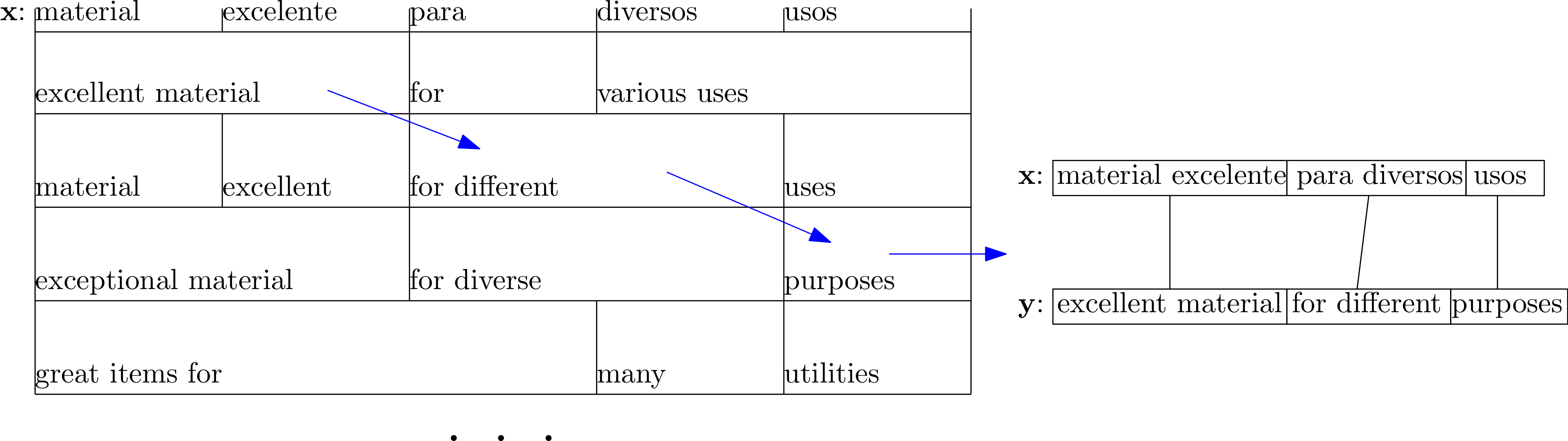
Given a set of translation options, it is typically possible to generate thousands or even millions of translations. The decoding process for SMT systems is defined so as to explore the search space of possible translations as efficiently as possible. To this end, the search algorithm generates partial hypotheses that are scored according to information contained in the statistical models. As a result of the decoding process, the hypothesis with the highest score is returned.

Partial Hypotheses

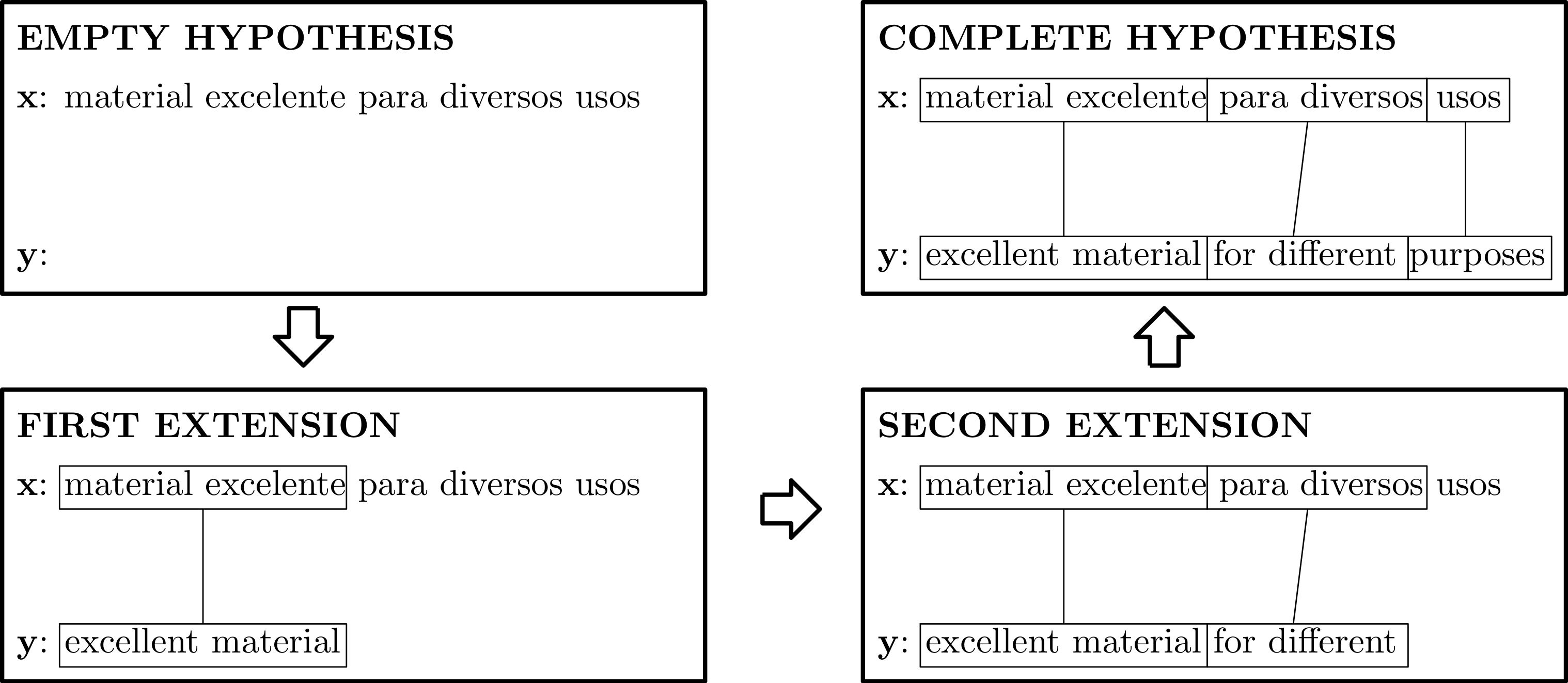
The search space is explored by creating partial hypotheses. Such partial hypotheses are extended incrementally, starting from the empty hypothesis, which contains no words. A new partial hypothesis is generated from a predecessor hypothesis by adding target words that translate a segment of the source sentence. We say that a hypothesis is complete when all of the words of the source sentence are translated by target language words. Below we show how a complete hypothesis can be built incrementally starting from the empty hypothesis.

Scoring

SMT finds the translation with the highest probability of being accurate for a given source sentence. Hence a mechanism to assign scores/probabilities to each hypothesis is necessary. In particular, hypotheses have an associated score which is revised after each extension. Let us consider the following extension example:

The hypothesis score is revised after the extension by adding the contributions of the phrase and language models:

• Phrase model: adds a score for translating material excelente with excellent material.

• Language model: adds a score for adding the words excellent material.

Search Algorithm

SMT systems work by incrementally extending partial hypotheses in an iterative process. The search algorithm uses a stack data structure that stores those hypotheses with higher scores nearer the top of the stack. Specifically, the algorithm executes the following steps:

1. Insert the empty hypothesis into the stack.
2. Remove the hypothesis with the highest score from the stack.
3. If the removed hypothesis is complete, then return it as a result and finish the algorithm. Otherwise, generate all possible extensions for the hypothesis and insert them into the stack.
4. Go to step 2.

Improving Decoding Efficiency

Typically, the search space to be explored during the translation of a given sentence is so large that the previously explained algorithm may become hopelessly slow. Here we explain two different techniques that can be applied to alleviate this problem, namely hypothesis recombination and stack pruning.

Hypothesis Recombination

Hypothesis recombination relies on the notion that sometimes two partial hypotheses cannot be distinguished by the SMT models in the sense that the extensions that can be applied to both of them are identical and add exactly the same score. Under these circumstances, we can discard (or recombine) the hypothesis with the lowest score without making the search algorithm sub-optimal.

Put more exactly, two hypotheses can be recombined if they share the same state in the SMT models. In our case, the state information is given by the language and phrase models. As it was explained in part I of this article, n-gram language models assign probabilities to each new word based on the previous (n-1) words. When the last (n-1) words of two hypotheses are the same, we say that they share the same state in the language model. On the other hand, phrase models only take into account the source segment being translated and the target translation when generating probabilities. Because of that, the phrase model state for a given hypothesis is determined by the positions of the words from the source sentence that have already been translated.

Below we show an example of two hypotheses, A and B, that can be recombined when assuming a 3-gram language model (the scores of the hypotheses do not come from real models but were chosen so as to illustrate how recombination works). As can be seen, the two hypotheses share the same SMT model states. On one hand, the last 2 words are the same for both hypotheses and thus they have the same language model state. On the other hand, they also share the same phrase model state since both translate the same source sentence positions. In this situation, hypothesis A can be safely discarded without preventing the algorithm from obtaining the optimal solution.

Stack Pruning

Another common way of improving the algorithm's efficiency is to limit the maximum number of hypotheses that can be stored into the stack. Whenever the limit is exceeded, the bottom of the stack is pruned. In contrast to hypothesis recombination, stack pruning may result in the algorithm producing a sub-optimal solution.

Decoding for Detokenization

In previous sections we explained how the decoding process for a general purpose SMT system works. This article focuses on using SMT systems for detokenization tasks. In this regard, the only difference with respect to conventional decoders is how the models are trained. Specifically, language and translation models should be trained following the instructions explained in part I. Once the models are appropriately estimated and given a tokenized input sentence, the decoding process explained above can be used without modification to obtain the detokenized sentence with the highest score.

Implementation Example

As it was explained in part I of this article, the detokenizer we propose is implemented by the Thot toolkit. More specifically, its functionality can be accessed by means of the thot_detokenize tool. thot_detokenize takes as input the text to be tokenized as well as the raw text file in the language of interest that is used for training the models:

thot_detokenize -f <tokenized_text> -r <raw_training_text>

It is possible to provide an additional file to thot_detokenize obtained as a result of tokenizing the raw text file with a particular tokenizer. When used in this way, the detokenizer learns how to detokenize from that sort of tokenizer instead of its native one (implemented by the thot_tokenize tool).

In the previous part of this article, we explained that thot_detokenize uses the Python tool thot_train_detok_model to train language and translation models. It is the thot_detok_translator tool that implements the decoding process described in this post, however. To find out additional details, readers can consult the Decoder class implemented in the thot_smt_preproc.py Python library, paying special attention to the expand and best_first_search functions.